technika

karnaughovy mapy

dnes jsem si při programování vzpomněl na školní léta, přesněji řečeno na ta středoškolská. při návrhu logických elektronických obvodů, který jsme sem tam museli učinit, často narazíte na logické funkce. taková logická funkce sestává z několika vstupů a jednoho výstupu, který se na základě těch vstupů mění. pokud se nemění, něco je špatně s hlavou toho, kdo funkci navrhoval. při návrhu elektroniky je třeba logické funkce minimalizovat, čímž se šetří hradla, která provádí jednotlivé logické součty a součiny. jak ale tu minimalizaci logické funkce provést ?

jedna z dobrých možností je znalost zákonů booleovy algebry. je dobré například vědět, že výraz A(A+B) nebo A+(AB) je vlastně vždy roven A nebo že když se někde při součinu vyskytne nula, je výsledek vždy nula a podobně. hodit se můžou i de morganovy zákony. pokud si je ale člověk nepamatuje nebo je líný je lovit z hlubin mysli, má ještě další možnost – použít karnaughovu mapu.

mapa se jmenuje po maurici karnaughovi, americkém fyzikovi. mě se zrovna přihodil onen případ s leností a tak jsem si na karnaughovu mapu vzpomněl. chvíli mi trvalo, než jsem si vybavil všechny detaily a s tím, jak se vlastně karnaughova mapa tvoří, mi pomohl až letmý pohled do wikipedie. neškodí si to tedy zopakovat. příspěvek na blog je dobrá forma opakování a navíc se tím vydá článek, což vede hned ke dvěma muším mrtvolám.

na svůj problém jsem narazil při parsování textu. potřeboval jsem vyřešit, zda je aktuální kus parsovaného textu ještě kus předchozího, nebo jde už o text nový. to ale není podstatné, podstatná je ona logická funkce, v mém případě obyčejná podmínka v programu. k dispozici byly tři boolean proměnné A, B a C. pokud je A i B true, podmínka platí, pokud je A i B false a k tomu C true, podmínka taky platí, pokud je A false a B true, podmínka taky platí a pokud je A true a B false, podmínka nemá být platná. z toho vyplývá následující tabulka možných výstupů z logické funkce:

A B C = X
1 1 0 = 1  zde nezáleží na proměnné C, proto jsou oba řákdy platné
1 1 1 = 1
0 0 0 = 0
0 0 1 = 1
0 1 0 = 1  ani zde není C důležité
0 1 1 = 1
1 0 0 = 0  a tady taky ne
1 0 1 = 0

řádky, kde je podmínka platná, odpovídají součinu a mezi nimi jde o logický součet, takže podoba funkce je AB + ^A^BC + ^AB = X, kde ^ označuje negaci a C občas v součinu chybí, protože jak je napsáno v tabulce, není důležité. když se to pokusíme zapsat v nějakém jazyce (např. C, které je mi sympatické), dostaneme

if ((A && B) || (!A && !B && C) || (!A && B)) { . . . }

což je odporně dlouhé. zjednodušit to nám pomůže mapa. ne ta topografická marsu, i když je moc pěkná, ale karnaughova. karnaughova mapa je vždy mapou dvojrozměrnou, takže její konstrukce je velice jednoduchá. v mém případě jde o tři proměnné, tak dvě umístím po vodorovné straně a jednu po straně svislé. můžeme to udělat i jinak, ale takhle je to hezčí. pro každou proměnnou po vodorovné straně potřebujeme dva sloupce, pro každou po svislé straně dva řádky, protože binární proměnné mohou nabývat jen dvou hodnot. pokud to někomu není jasné a přesto dočetl až jsem, je na místě ho upozornit, že i když bude pokračovat, nic o justinovi bieberovi se tu nedočte. máme tedy dvě proměnné vodorovně, to dělá čtyři sloupce a dvě proměnné svisle, to dělá dva řádky. v tomto bodě bude dobré si mapu ukázat.

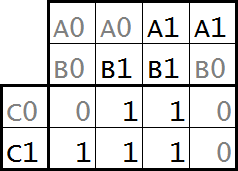
vodorovně je první proměnná A, pod ní B. v polích jsou napsány hodnoty, kterých proměnná nabývá. všimněte si, že výpis hodnot proměnné B je oproti proměnné A pootočen. to je důležité, dostaneme tak pod sebe všechny možné kombinace hodnot – A=0 B=0, A=0 B=1, A=1 B=1, A=1 B=0. pootočení si lze představit, jako by šlo o čtyřbitový registr a já provedl jeho rotaci vlevo, i když levičák nejsem. kdybych provedl rotaci vpravo, nebude to mít na funkci mapy žádný vliv. to samé platí pro proměnné, které mají hodnoty svisle, ale my máme jen C a tak tu není co rotovat. co znamenají ty nuly a jedničky ve zbývajících polích ? jsou to výsledky funkce opsané z výše uvedené tabulky. pokud je A=1, B=1 a C=0, jde o třetí buňku v prvním řádku (hlavičkové sloupce ani řádky nepočítám) a tak tam z tabulky opíšeme 1. pokud je A=1, B=1 a C=1, jde o třetí buňku ve druhém řádku a tam taky opíšeme jedničku atd.

teď je čas přistoupit k vlastní minimalizaci logické funkce. zní to hrozně, ale protože se to dělá graficky, bude to jednoduché a pěkně barevné. v mapě najdeme skupiny jedniček. jak taková skupina vypadá ? musí to být čtverec nebo obdélník, jehož hrana může být dlouhá dvě nebo čtyři pole. proč ? jde o mocniny dvojky. máme nanejvýš pohromadě dvě proměnné (ty vodorovné), takže připadají v úvahu čísla 2¹ a 2², což je právě 2 a 4. dalším pravidle pro tvoření skupin je, že musejí být co největší (čím větší skupina, tím větší minimalizace) a že se mohou překrývat, ale ne zcela pohlcovat. posledním pravidlem je, že musíme najít všechny. také je třeba mít na paměti, že mapa je jakoby spojená, tedy i případné jedničky, které jsou úplně vlevo a ve stejném řádku i úplně vpravo, jsou vlastně vedle sebe. jedničky úplně nahoře a úplně dole ve stejném sloupci jsou taky vedle sebe.

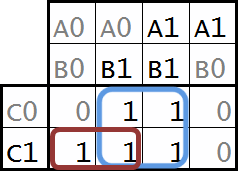
jak je vidět, v téhle mapě jsou jen dvě skupiny jedniček. jedna velká, modrá a jedna malá, červená. jiné skupiny vytvořit nejdou, díky výše uvedeným pravidlům. nyní se konečně dostáváme k tomu zázraku, budeme minimalizovat. soustředíme se nejdříve na velkou modrou skupinu, podíváme se na hodnoty proměnných. pokud se hodnota proměnné, která spadá do skupiny, mění, můžeme ji vypustit. znamená to totiž, že ať je její hodnota 0 nebo 1, na výsledek funkce to nemá vliv, ten bude pořád 1. proměnná, která se v rámci skupiny nemění, naopak důležitá je. je z toho patrno, že může nabýt jen jedné určité hodnoty, aby funkce měla kýžený výsledek, tedy 1. v rámci velké modré skupiny mění proměnná A svojí hodnotu, takže ji zanedbáme. proměnná B nabývá jen hodnoty 1, takže tu si necháme a proměnná C se také mění, takže na ni taky kašleme. proměnné, které zbyly, se zapisují v součinovém tvaru. nám zbyla jen jedna, tak zapíšeme B. v malé červené skupině je trvalou hodnotou proměnná A, protože nabývá jen hodnoty 0 a proměnná C, která nabývá jen hodnoty 1. proměnná B se mění a tak na ní kašleme. zapíšeme tedy součin ^AC, kde A je negováno, protože jeho neměnná hodnota v rámci malé červené skupiny je 0 a my chceme 1. obecně vzato, z každé skupiny, ať je jakkoliv velká a má jakoukoliv barvu, nám vypadne nějaký součin. součet všech součinů je pak výslednou hledanou zjednodušenou funkcí a ta v našem případě vypadá jako B + ^AC. zapsáno jako podmínka, dostaneme mnohem sympatičtější

if (B || (!A && C))

no nebyla to legrace ? abych výklad nějak dokončil, uvedu v posledním obrázku ještě příklad skupiny, která jde přes okraje tabulky. jde o úplně stejnou funkci a tedy i stejnou karnaughovu mapu, jen je trochu pootočená (sakra, zas vlevo).

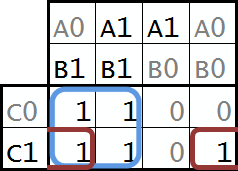
doufám, že je to jasné. ti, co to dočetli omylem, se alespoň dozvěděli, že tu skutečně nic o justinovi bieberovi není a těm ostatním přeji pěknou zábavu při karnaughově mapování.